At the meet Tuesday, I was talking with Sabre and the good Doctor about motor elasticity: a term that appears often in German publications on cars, but that I've never seen in English. I did my best to describe it to them, but came up short. So, I present today, the German Wikipedia snippet translated in English. It is fairly succinct and clear, but I am happy to clarify and questions regarding the phrasing. Please forgive my poorly formatted math equations. The italics are my emphasis are for keywords. Sidenote: the poor elasticity of a 600cc sportbike (despite being crazy fast) is the reason why immature 18-yo's think they need a liter bike at minimum. Alright, I'm done yelling at the clounds.
Elasticity (automotive technology)
Elasticity of a motor vehicle powertrain describes the condition where the rated RPM of a powerplant is greater than the RPM at which the unit creates its greatest torque; the rated RPM is the RPM at which the rated output (RJ's note: in this case, horsepower) is produced. During an increase in load (in the sense of an increase in driving resistance) such as going uphill or driving into a headwind, this allows you -not- to downshift as your speed falls, due to an increase in torque. The farther the RPM of the maximum torque is (relatively) removed from the RPM of maximum output, the more elastic the motor is.
Calculating Elasticity
For motor elasticity, a distinction is drawn among torque elasticity, RPM elasticity, and the total elasticity of a motor.
Torque elasticity
eMd = Md2/Md1
Where Md1 is the torque at maximum HP and Md2 is maximum torque
RPM elasticity
en = n1/n2
Where n1 is the RPM at maximum output (rated RPM) and n2 is RPM at maximum torque
Total motor elasticity
E = eMd * en = Md2/Md1 * n1/n2
Sometimes RPM elasticity is called "total elasticity" and torque elasticity is called "motor elasticity"; n1 - n2 describes the "elastic range"
Examples of various RPM elasticities:
Puch-Motorcyle (post-war model), gasoline, 1.01 (not elastic)
Dodge Viper R/T 10, gasoline, 1.28
Honda motorcycle (modern sportbike), gasoline, 1.40
Steyr tractor (modern), diesel, 1.57
Opel Vectra A 2.0i, gasoline, 1.93
Mercedes 220 CDI, diesel, 2.10
VW Golf V R32, gasonline, 3.10 (very elastic)
Series-wound electric motors and steam motors, that have their maximum torque available at an RPM of 0, and therefore usually forego transmissions, are considered particularly elastic.
Motor elasticity
Moderator: Moderators
- snaab
- DCAWD Groupie
- Posts: 2149
- Joined: Tue May 30, 2006 5:51 pm
- Location: West Hollywood, CA
Motor elasticity
RJ
'13 Mazda3
'13 Mazda3
- PGT
- DCAWD Groupie
- Posts: 1578
- Joined: Mon Jun 04, 2007 11:06 am
- Location: Loudoun
Re: Motor elasticity
interesting. I've seen a stat where 30-80 or similar is measured in top gear to judge tractibility. Ex for '12 BMW 328i manual:
Top gear, 30–50 mph: 9.9 sec
Top gear, 50–70 mph: 7.6 sec
Top gear, 30–50 mph: 9.9 sec
Top gear, 50–70 mph: 7.6 sec
2013 BMW 328i M Sport with 8sp in Estoril Blue II
2012 Chrysler 300C SRT8 - Always bet on black
2012 Jeep Wrangler Unlimited Rubicon Call of Duty: Modern Warfare 3 Edition, otherwise known as the MW3 (and badass)
2012 Chrysler 300C SRT8 - Always bet on black
2012 Jeep Wrangler Unlimited Rubicon Call of Duty: Modern Warfare 3 Edition, otherwise known as the MW3 (and badass)
- snaab
- DCAWD Groupie
- Posts: 2149
- Joined: Tue May 30, 2006 5:51 pm
- Location: West Hollywood, CA
Re: Motor elasticity
Hm, I had forgotten that is given in some reviews. It always seemed a little arbitrary to me though. I guess I'd rather look at a number. A friend just bought a Speed3 over an FR-S, becuse the FR-S was too slow. When I pointed out that the 0-60 time was less than a second slower, I also indicated that the Speed3 probably -felt- faster because it's so much torquier (and therefore more elastic due to the turbo).
RJ
'13 Mazda3
'13 Mazda3
- drwrx
- DCAWD Founding Member
- Posts: 4382
- Joined: Mon Sep 20, 2004 8:00 pm
Re: Motor elasticity
Thanks for doing the digging and for the clear explanation.
Although using the formula in conversation would have gotten a dear in the headlights look from me.
This is perfect.Torque elasticity
eMd = Md2/Md1
Where Md1 is the torque at maximum HP and Md2 is maximum torque
Although using the formula in conversation would have gotten a dear in the headlights look from me.
- snaab
- DCAWD Groupie
- Posts: 2149
- Joined: Tue May 30, 2006 5:51 pm
- Location: West Hollywood, CA
- PGT
- DCAWD Groupie
- Posts: 1578
- Joined: Mon Jun 04, 2007 11:06 am
- Location: Loudoun
Re: Motor elasticity
true about relative feeling of speed. my E550 Coupe felt faster than my SRT8, but I chalk that up to having SO much torque available so low in the range. The SRT8 has a higher peak torque figure but it comes on much later (and the car is some 700lbs heavier being a sedan based on the E211 E Class chassis vs. the E550 which is based on the W204 C Class chassis).
I think objective performance measures are pretty close (1/4 mile, 0-60, etc).
I think objective performance measures are pretty close (1/4 mile, 0-60, etc).
2013 BMW 328i M Sport with 8sp in Estoril Blue II
2012 Chrysler 300C SRT8 - Always bet on black
2012 Jeep Wrangler Unlimited Rubicon Call of Duty: Modern Warfare 3 Edition, otherwise known as the MW3 (and badass)
2012 Chrysler 300C SRT8 - Always bet on black
2012 Jeep Wrangler Unlimited Rubicon Call of Duty: Modern Warfare 3 Edition, otherwise known as the MW3 (and badass)
- Sabre
- DCAWD Founding Member
- Posts: 21432
- Joined: Wed Aug 11, 2004 8:00 pm
- Location: Springfield, VA
- Contact:
Re: Motor elasticity
Very interesting notion! I have to say, I've never heard an equivalent in Amurican terms 
VERY interesting! I would have thought the Viper would be much higher because of the mounds of torque it produces!snaab wrote: Examples of various RPM elasticities:
Puch-Motorcyle (post-war model), gasoline, 1.01 (not elastic)
Dodge Viper R/T 10, gasoline, 1.28
Honda motorcycle (modern sportbike), gasoline, 1.40
Steyr tractor (modern), diesel, 1.57
Opel Vectra A 2.0i, gasoline, 1.93
Mercedes 220 CDI, diesel, 2.10
VW Golf V R32, gasonline, 3.10 (very elastic)
Sabre (Julian)

92.5% Stock 04 STI
Good choice putting $4,000 rims on your 1990 Honda Civic. That's like Betty White going out and getting her tits done.

92.5% Stock 04 STI
Good choice putting $4,000 rims on your 1990 Honda Civic. That's like Betty White going out and getting her tits done.
- drwrx
- DCAWD Founding Member
- Posts: 4382
- Joined: Mon Sep 20, 2004 8:00 pm
Re: Motor elasticity
I suspect it's the torque/hp split that kills the Viper. High hp at high rpm vs high Torque at low rpm. A dyno plot with the crossover might make it move obvious.Sabre wrote:VERY interesting! I would have thought the Viper would be much higher because of the mounds of torque it produces!
- Sabre
- DCAWD Founding Member
- Posts: 21432
- Joined: Wed Aug 11, 2004 8:00 pm
- Location: Springfield, VA
- Contact:
Re: Motor elasticity
Viper and ZR1 as you requested 
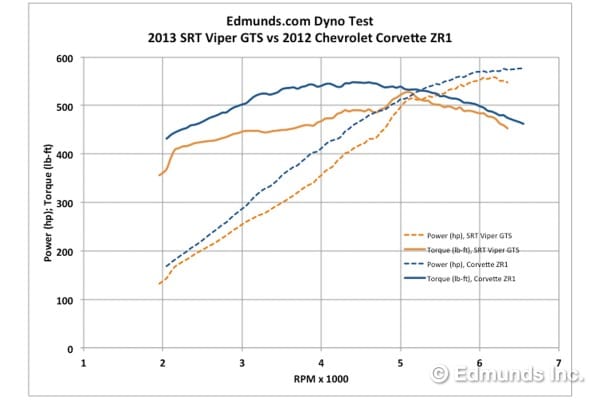
hmmmm.... One thing I will say.... the viper needs another tune. That is lumpy!

hmmmm.... One thing I will say.... the viper needs another tune. That is lumpy!
Sabre (Julian)

92.5% Stock 04 STI
Good choice putting $4,000 rims on your 1990 Honda Civic. That's like Betty White going out and getting her tits done.

92.5% Stock 04 STI
Good choice putting $4,000 rims on your 1990 Honda Civic. That's like Betty White going out and getting her tits done.
- drwrx
- DCAWD Founding Member
- Posts: 4382
- Joined: Mon Sep 20, 2004 8:00 pm
Re: Motor elasticity
Crossover point at around 5,200 RPMs for both.
I guess I see the formula at work.
I guess I see the formula at work.